石剑云,潘科
(大连交通大学土木与安全工程学院,辽宁大连116028)
摘要:针对沸腾液体膨胀蒸汽爆炸(BLEVE)的两个主要危害:冲击波、抛射物进行后果预测研究。在其他研究者液化气储罐火灾实验研究的基础上,基于BLEVE冲击波超压可用能由“膨胀蒸汽”单独提供的假设,建立了冲击波超压与”膨胀蒸汽“能量之间的关系式。在其他研究者过热液体容器水平火箭式抛射实验的基础上,基于飞出物动能与过热液体的过热能成比例的假设,建立了火箭式抛射物初速与过热液体过热能之间的关系式。通过计算实例证明这两种方法都比较合理。
关键词:沸腾液体膨胀蒸汽爆炸;冲击波;超压;碎片
引言
沸腾液体膨胀蒸汽爆炸(Boiling Liquid Expanding Vapor Explosion,简称BLEVE)是液化气容器可能发生的危害性最大的事故之一。这种事故可简单表述如下:液化气在密闭容器内处于常压以上的气液平衡状态,若容器突然完全破裂(可能由于火灾侵袭、猛烈撞击、容器腐蚀失效等原因)造成压力骤降,这种平衡则被打破,引发“沸腾液体”和“膨胀蒸汽”的爆炸性释放。锅炉中的水蒸汽爆炸与其原理相同,大部分研究者将锅炉的水蒸汽爆炸也纳入BLEVE的范畴。
BLEVE事故会造成两个直接危害:冲击波、抛射物。如果介质可燃,可能会形成火球或蒸气云爆炸;如果介质有毒有害,则会形成有毒、有害物的扩散。本文只研究BLEVE物理爆炸形成的冲击波和抛射物后果。
冲击波的破坏力大小主要是由冲击波超压决定的。冲击波超压的预测一般有数值计算、简单计算两种方法[1-5]。本文采用简单计算的方法,即根据介质前后的热力学状态推算出爆炸释放能,进而预测出冲击波超压,其关键是冲击波可用能的确定。
BLEVE产生的碎片危害距离要比冲击波大得多,易造成人员伤亡和引发二次事故。现在有一些研究者进行了相关的理论和实验研究[1,6,7]。由于碎片抛射后果的随机性较大,本文只针对一种典型事故形式下的飞出物初速进行预测。
1 BLEVE冲击波可用能的确定
估算冲击波超压的关键是先确定产生冲击波的能量。当容纳过热液体的压力容器发生完全破裂时,能量的释放源为“膨胀蒸汽”和“沸腾液体”,释放出的能量有一部分产生了冲击波。当前大部分研究者假
定冲击波可用能由“膨胀蒸汽”和“沸腾液体”共同提供,总能量的一部分转化为冲击波可用能。
但随着BLEVE研究的不断进展,对于冲击波能量源的问题一些研究者有了不同的观点。一些研究者通过实验研究发现用“膨胀蒸汽”和“沸腾液体”的总释放能作为冲击波的能量源得出的超压计算值远大于实验值。加拿大女王大学的Birk教授在持续十几年的液化气储罐火灾试验的基础上,得出冲击波可用能只由“膨胀蒸汽”单独提供的结论[8]。
Birk通过大量实验研究认为,过热液体的沸腾发生在容器破裂之后,其相变速度还不够快到产生冲击波的地步,即使液体温度超过其过热极限温度也是如此。液体沸腾释放出的能量大部分作用于碎片抛射、容器附近破坏、辅助蒸汽撕裂容器等,但不会产生冲击波作用于容器的远场。具体数据及分析可参考文献。
虽然BLEVE理论的开创者Reid将BLEVE定性为过热液体达到过热极限后发生的均匀核化沸腾29.但众多研究结果表明完全遵守该定义的BLEVE几乎没有8。锅炉过热水的温度远低于其过热极限温度,依然会发生强烈的物理爆炸。而且,有关研究人员在不同介质、过热度、容器等多种条件下进行过热液体泄压爆沸实验,都发现过热液体的爆沸是一个逐步发展的过程,很少出现整体的均匀核化沸腾[9-11]。Van den Berg等人用数值计算的方法预测BLEVE冲击波超压,认为只有当容器瞬间完全破裂时过热液体才会产生强的冲击波,一旦容器的破裂稍微延缓一点儿,冲击波就非常弱了[5]。这些都说明过热液体泄压后爆沸会释放能量,但释放速度可能还不足以形成冲击波。
虽然BLEVE冲击波能量源问题还没有定论,但考虑Birk等人的观点有较多的实验数据支持,而且为了与常用方法进行对比研究,本文假设冲击波可用能由“膨胀蒸汽”单独提供。
2 本文采取的冲击波超压预测方法
2.1冲击波估算的假设条件
(1)冲击波可用能由“膨胀蒸汽”单独提供。
(2)同类型的BLEVE事故,冲击波可用能与“膨胀蒸汽”释放能之间有一较稳定的比例关系。
2.2计算过程简介
(1)确定蒸汽释放能
容器突然破裂时,蒸汽视为理想气体绝热可逆膨胀,其释放能可用式(1)计算。
Eg = PV /(k-1)I1- (101.3/ P)(k-1)/k] (1)
式中,Eg为气体的释放能,KJ;P为容器内气体的绝对压力,kPa;V为容器内气相体积;k为气体的绝热指数,即气体的定压比热与定容比热之比。
(2)确定冲击波可用能
由于假设蒸汽为理想气体绝热可逆膨胀会大大高估其实际释放能[3,4],且蒸汽释放出的能量只能有一部分作用在冲击波上。假设由(1)式得出的冲击波可用能与”膨胀蒸汽”释放能之间有一较稳定的比例关系,则冲击波可用能可由式(2)得出。比例系数根据实验数据推得。具体方法将在2.3节介绍。
Eex = X·Eg (2)
(3)求得能量比拟距离[1,2]
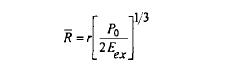
Eex前的系数2是考虑了水平面爆炸形成的冲击波为半球状扩展,比球形扩展能量更集中;Ṝ为能量比拟距离;r为目标距爆炸中心距离,m;P0为环境大气压,kPa;
根据美国化工过程安全中心(CCPS)的建议,考虑地面反射和容器的形状因素,由式(3)求得的Ṝ应乘以一个系数β进行修正[1],β取值见表1。

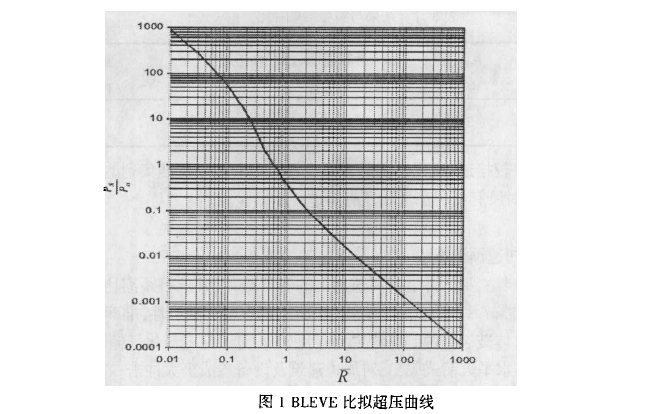
(4)借助比拟超压曲线查得冲击波侧向超压峰值[2]
图1中横坐标为能量比拟距离Ṝ.由比拟超压曲线可查到该点冲击波超压与环境大气压之比Ps/P。,即可得出冲击波侧向超压峰值Ps。
2.3冲击波可用能与”膨胀蒸汽”释放能比例系数的获得
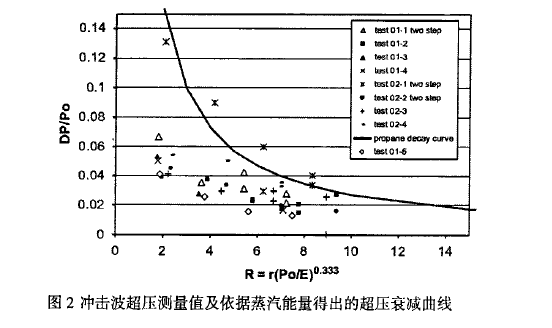
Birk在2002-2004年做了一系列2000L丙烷储罐的火灾试验。在这些火灾试验中有一部分储罐发生了BLEVE,获取了一些距离下的冲击波超压数据,测点超压值如图2[8]。Birk用蒸汽等熵膨胀的能量得到冲击波衰减曲线,完全能够解释获得的冲击波超压。本文依据文献[中给出的数据推出冲击波可用能与“膨胀蒸汽”释放能之间的比例系数。
根据图2中的所有实测点和理论衰减曲线推得每组实验的能量比例系数,统计得x=0.55,即蒸汽等熵膨胀的能量有55%产生了冲击波,该系数在0.95置信水平下的置信区间为[0.47,0.63]。
2.4实例验证
德国BAM机构的Balker1999年进行过一次全尺寸的铁路罐车火灾试验8,其储罐及介质初始条件如表2。

用2.2节介绍的方法进行计算,计算结果与实验结果如表3。
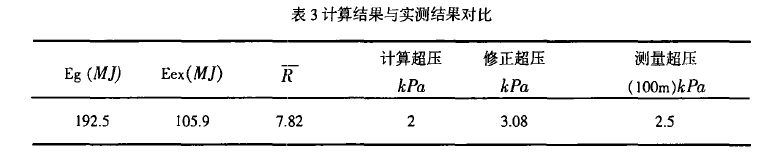
可看出计算结果和测量结果较接近,说明本文的方法比较合理。由于可搜集到的BLEVE冲击波超压数据有限,本文提供的方法是否对所有情况都适用还有待进一步检验。
3 容器抛射物初速预测
3.1基于能量转化的容器抛射物初速预测方法
除了冲击波,BLEVE的另一个主要危害是其高速抛出的容器碎片,其危害距离比冲击波大得多,易造成人员伤亡和引发二次事故。容器碎片的形式、轨迹和抛出距离都有很大随机性,准确预测很困难。但对于大多数BLEVE事故,容器一般整体破裂为两到三块主要碎片AI2。对于卧式液化气储罐及锅炉锅筒较典型的一种事故形式是封头连带筒体水平火箭式飞出,对周边建筑及设备造成极大冲击。本文针对这种事故形式进行研究,预测失效容器火箭式飞出时的初速。
由于容器内过热液体能量多且作用时间长,大多研究者在估算飞出物初速时只考虑液相提供的能量[2.7]。液体过热能(相对常压沸点温度)可由公式(4)估算[2]。
E=mCp(T-Tb) (4)
式中m为液体质量,kg;Cp为液体定压比热,忽略随温度变化;T为容器失效前液体温度,℃;Tb为液体在环境压力下沸点,℃。
假设飞出物获得的动能与容器内液体过热能成正比,则飞出物初速可由公式(5)估算
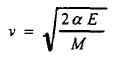
式中v为飞出物初速,m/s;E为容器内液体过热能,J;M为飞出物质量,kg;α为容器内介质能量转化为飞出物动能的比例系数,由实验数据推出。
Baum(1999)做了大量卧式储罐水平抛射实验,实验条件为容纳过热水的圆筒容器一端固定,端部断裂后封头连带筒体水平飞出[7],实验数据见表4。对于失效容器火箭式飞出,这是一种最危险的情况,本文以此为依据推算飞出物初速。

由公式(5)推得每组实验的能量比例系数,统计得α=0.0054,即有0.54%的过热能转化为了飞出物动能。该系数在0.95置信水平下的置信区间为[0.0042,0.0065]。
3.2实例验证
Hunt,&Wood1987年用水做过类似实验[7],只是储罐、实验温度与前者不同。实验条件及结果如表5。

用3.1节介绍的方法进行计算,实验1、2的飞出物初速理论计算值分别为37.14m·s-1和49.9m·s-1,与实验测量值接近,说明此方法较合理。实际应用时根据卧式储罐内介质的过热能和飞出物的质量即可估算出飞出物水平初速。
4 结论
(1)基于“冲击波可用能由膨胀蒸汽单独提供”和“同类事故中冲击波可用能与膨胀蒸汽释放能之间比例关系较稳定”的假设,本文提出了一种BLEVE冲击波超压预测方法,综合了大量实验数据,得出了给定
距离下冲击波侧向超压峰值与容器蒸汽能量的关系式。通过实例证明该方法较为合理。
(2)针对卧式储罐BLEVE事故中整体水平火箭式飞出的情况,假设飞出物动能与液体过热能成正比,基于前人的实验数据,得出飞出物初速与液体过热能之间的关系式。通过实例证明该方法较为合理。
(3)本文提出的方法简单易用,可为风险评估和事故救援提供参考,但其适用性还需要更多的案例进一步验证。
参考文献
[1] Tasneem Abbasi, S.A. Abbasi. The boiling liquid expanding vapour explosion (BLEVE): Mechanism, consequence assessment,management[J]. Journal of Hazardous Materials, 2007,141(3): 489-519.
[2] B. Genova, M. Silvestrini, FJ. Leon Trujillo. Evaluation of the blast -wave overpressure and fragments initial velocity for a BLEVE event via empirical correlations derived by a simplified model of released energy [J]. Journal of Loss Prevention in the Process Industries, 2008,21(1): 110–117.
[3] G.A. Pinhasi, A. Ullmann, A. Dayan. ID plane numerical model for boiling liquid expanding vapor explosion(BLEVE)[J]. Interna-tional Journal of Heat and Mass Transfer, 2007,50(23–24):4780–4795.
[4] E. Planas-Cuchi, J. M. Salla, J. Casal. Calculating overpressure from BLEVE explosions[]]. Journal of Loss Prevention in the Pro-cess Industries, 2004,17(6):431–436.
[5] A. C. van den Berg, M. M. van der Voort, J. Weerheijm, N. H. A. Versloot. Expansion–controlled evaporation: a safe approach to BLEVE blast[J]. Joumal of Loss Prevention in the Process Industries, 2004,17(6): 397–405.
[6] A. M. Birk. Hazards from propane BLEVEs: An update and proposal for emergency responders [J]. Journal of Loss Prevention in the Process Industries,1993,9(2):173–181.
[7] M. R. Baum. Failure of a horizontal pressure vessel containing a high temperature liquid: the velocity of end–cap and rocket mis-siles[J]. Joumal of Loss Prevention in the Process Industries, 1999,12(2): 137-145.
[8] A.M. Birk, C. Davison, M. Cunningham. Blast overpressures from medium scale BLEVE tests[]]. Journal of Loss Prevention in the Process Industries, 2007,20(3): 194–206.
[9] Riccardo Barbone. Explosive boiling of a depressurized volatile liquid[D]. McGill University.1997.
[10] Hill,L.G.. An Experimental Study of Evaporation Waves in a Superheated Liquid[D]. Califomia Institute of Technology.1991.
[11] Hahne E, Barthau G.. Evaporation waves in flashing processes[]]. Internation Journal of Multiphase Flow,2000,26(4):531-547.



