胡昆,陈国华,周志航,黄孔星
(华南理工大学安全科学与工程研究所,广东 广州 510641)
摘要:爆炸冲击波是导致化工园区多米诺效应事故升级的重要原因之一。在文献分析的基础上,本文从爆炸冲击波强度表征、化工设备破坏失效的动力响应、破坏失效概率计算方法、易损性分析等4个方面,指出目前爆炸冲击波作用下化工设备易损性研究存在的不足,进而提出了进一步研究方向,包括不同爆炸类型的超压时程曲线特征与能量频谱规律研究、空间分布参数模型或集中参数模型的定量研究、基于结构可靠性的破坏失效概率计算方法、爆炸冲击波强度参数与设备抗性参数的易损性分析等,在此基础上系统性建立了爆炸冲击波作用下化工设备易损性研究的流程图,指出集中参数的可靠性方法与随机有限元法是爆炸冲击波作用下化工设备易损性研究的关键性方向,为提高爆炸冲击波多米诺效应定量风险评估的可靠度与精确度提供参考。
关键词:爆炸冲击波;多米诺效应;设备易损性;集中参数的可靠性方法;随机有限元法
中图分类号:TQ 086;X 937 文献标志码:A 文章编号:1000-6613(2019)04-1634-12
Review of the vulnerability of chemical equipment subjected to blast wave
HU Kun,CHEN Guohua,ZHOU Zhihang,HUANG Kongxing
(Institute of Safety Science and Engineering, South China University of Technology, Guangzhou 510641,Guangdong, China)
Abstract: Blast wave is one of the important escalation factors of Domino effect in chemical industryparks. Based on the literature analysis, the inadequacies of current research on vulnerability of chemicalequipment subjected to blast wave were pointed out, from the four aspects of the intensity characterizationof blast wave, the dynamic response of equipment damage, the damage probability of equipment and thevulnerability analysis. It was suggested that the characteristic of overpressure history curve and energyspectrum about different explosion types, quantitative study on spatial distribution parameter model orlumped parameter model, damage probability methods based on the structural reliability and thevulnerability analysis of blast wave intensity parameters and equipment resistance parameters should befurther studied. Based on these, the flow chart of the vulnerability of chemical equipment subjected toblast wave was built. The critical sections of equipment vulnerability analysis were the reliability methodof lumped parameter and stochastic finite element method. The review can be considered as the referencefor enhancing the reliability and accuracy of quantitative risk assessment of domino effect.
Key words: blast wave; Domino effect; equipment vulnerability; reliability method of lumped parameter;stochastic finite element method
收稿日期:2018-04-11;修改稿日期:2018-05-25。
基金项目:国家自然科学基金(21576102)。
第一作者:胡昆(1993—),男,博士研究生,研究方向为工业安全与风险评价技术。
通信作者:陈国华,教授,博士生导师,研究方向为工业安全与风险评价技术、过程装备安全可靠性及风险评价技术。
引用本文:胡昆, 陈国华, 周志航, 等. 爆炸冲击波作用下化工设备易损性研究评述[J]. 化工进展, 2019, 38(4): 1634-1645.
Citation:HU Kun, CHEN Guohua, ZHOU Zhihang, et al. Review of the vulnerability of chemical equipment subjected to blast wave[J]. Chemical Industry andEngineering Progress, 2019, 38(4): 1634-1645.
在多米诺效应事故中,初始事故可能通过火灾热辐射、爆炸冲击波、爆炸碎片等物理效应作用毗邻的化工设备或装置,导致多米诺效应事故的发生,进而增加了后果严重性或失效频率[1]。多米诺效应的核心是事故扩展传播与后果影响扩大[2],而爆炸冲击波是导致多米诺效应事故升级的重要因素之一。Delvosalle[3]通过事故统计发现,16.5% 的多米诺效应事故是由爆炸冲击波超压造成的 。MHIDAS数据库显示,由爆炸引起的105起固定设备多米诺效应事故中,66 起波及到了临近设备或装置[4]。当前,关于爆炸冲击波引发多米诺效应事故的研究主要集中在冲击波超压破坏化工设备概率方面,主要采用基于事故数据的统计方法。然而,由于方法的局限性,数据统计忽略了实际中冲击波与设备之间的动力响应过程。
设备破坏失效概率计算方法是爆炸冲击波多米诺效应定量风险评估的关键要素[5]。在多米诺效应事故场景中,爆炸冲击波破坏化工设备的影响因素包括3类[6]:一是爆炸冲击波的强度,主要有静态峰值超压、动态压力 (曳引力)、正相持续时间、冲量等强度参数;二是设备的抗冲击能力,主要有材料特征、几何尺寸、设计压力、结构自振周期等抗性参数;三是爆炸冲击波与化工设备之间相互作用的复杂现象 (即动力响应),主要有爆炸冲击波与设备之间的空间关系 (或相对位置)、爆炸冲击波反射、绕流、流体分离等。其中,复杂现象过程体现了设备的抗冲击能力。因此,为了爆炸冲击波多米诺效应定量风险评估更加可靠、精确,从爆炸冲击波强度表征、化工设备破坏失效的动力响应、破坏失效概率计算方法、易损性分析4个方面进行评述,梳理爆炸冲击波作用下化工设备易损性研究存在的不足,并提出进一步研究方向。
1 爆炸冲击波破坏强度表征方法
1.1 化工园区爆炸冲击波多米诺效应事故场景
化工园区中,引发爆炸冲击波多米诺效应的初始事故场景主要包括蒸气云爆炸(VCE)、沸腾液体扩展蒸气爆炸 (BLEVE)、约束爆炸 (设备或建筑中的气体、蒸气或粉尘爆炸等)、机械爆炸 (容器破裂等)、凝聚相爆炸等[7]。不同爆炸类型引发多米诺效应事故升级的因素不同,可能产生的二级事故场景也存在很多的可能性,主要取决于设备存储介 质 的 危 害 性 。2005 年 , Cozzani 等[6]通 过 对MHIDAS 数据库的 105 起多米诺效应事故进行统计,得出不同爆炸类型引发多米诺效应事故升级的因素及可能产生的二级事故场景,见表1。在爆炸冲击波作用下设备易发生强度屈服、倒 塌、破裂、分解、整体位移等破坏失效。考虑爆炸冲击波的远场破坏,化工设备常发生的爆炸类型主要以VCE、BLEVE、凝聚相爆炸为主[8]。

1.2不同爆炸类型的爆炸冲击波强度计算方法
在爆炸后果的定量风险评估中不同爆炸类型的爆炸冲击波强度计算方法,一个通用性假设是爆炸事故产生的爆炸冲击波可比为等效当量的炸药产生的理想爆炸冲击波,与爆炸类型无关,即在远场范围内,任意类型爆炸产生的爆炸冲击波是相似的。在爆炸冲击波的远场作用或爆炸冲击波压力较低时,动态超压可以忽略,只考虑静态峰值超压。但是不同爆炸类型产生的爆炸冲击波有着不同的强度计算方法。
(1)VCE
VCE 定义为易燃蒸气、瓦斯、喷雾等与空气的预混气云引燃后的爆炸。在爆炸过程中火焰加速到足够高的速度产生显著的超压,即使在较远的距离也能引发多米诺效应。计算方法[9]包括物理模型、VCE关系模型的爆炸冲击波强度、数值模拟方法,其中关系模型应用最为广泛,有 TNT 当量法[10]、TNO多能法[11]、Baker-Strehlow法[12]等,关系模型的对比分析见表2。

TNT当量法的核心思想是将可燃蒸气云燃烧释放的能量转化为释放相同能量的 TNT 炸药当量,从而利用TNT的爆炸效应预测VCE。TNT当量法存在近距离超压接近无限大的问题,对近场预测结果存在过高估计。因此,TNT 当量法仅适用远场预测,存在点源位置与可燃气云的当量系数α难以确定、TNT 高能炸药爆炸与 VCE 存在本质区别等问题。沙金成[13]、严景艺等[14]、管义锋等[15]、丁宇奇等[16]分别应用TNT当量法预测蒸气云爆炸超压及事故后果。
TNO 多能法与Baker-Strehlow 法相似,采用的是气体爆炸模型且使用Sachs比例规律进行参数量纲为1化处理,核心思想是蒸气云爆炸只有在部分约束很强的条件下才能产生强的冲击波。区别在于分别通过爆源强度、马赫数Ma确定TNO或BakerStrehlow曲线。1997年,Mercx等[17]在《黄皮书》中指出:TNO 多能法建立了爆炸冲击波超压、正相持续时间与距离的函数。2000年,Mercx等[18]基于实验数据推导出 TNO 多能法的爆源强度联合参数关系式,用于指导爆源强度的选择。Maremonti等[19]、Lobato等[[20]、Salzano等[[21]应用TNO多能法进行蒸气云爆炸事故后果评估和多米诺效应风险分析。2006 年,Alonso 和 Ferradás 等[22-24]在 TNO 多能法基础上建立了VCE的超压-冲量-距离特征曲线,更加简捷地确定爆炸冲击波的超压与冲量。1979年,Strehlow 等[12]提出了球形 VCE 爆炸的 Baker -Strehlow方法。1999年,Tang与Baker[25]提出包含爆炸冲击波正负相参数的改进 Baker-Strehlow 曲线,使爆轰、超声爆燃及次声火焰等情况下的预测更准确。
TNT 当量法、TNO 多能法、Baker-Strehlow 法主要是对爆炸冲击波超压进行预测,表3列出了已有的3种方法超压预测结果的对比分析研究。由表3可知,当距离爆源较近时,TNT当量法预测的超压大于其他两种方法;当距离爆源较远时,3种方法的预测结果相近。

(2)BLEVE
由表1可知,相对于VCE,BLEVE的机械效应不用考虑火球的复杂影响,事故升级因素主要包括爆炸冲击波和碎片[28]。BLEVE的爆炸冲击波强度计算方法包括经验公式法、数值方法。
经验公式法的计算过程分为两部分:①计算BLEVE产生的机械能量(即爆炸总能量)E及爆炸冲击波能量 Ew;②通过 Ew计算爆炸冲击波超压。基于不同的热力学和物理假设,不同学者提出了不同的BLEVE机械能量计算方法,见表4。这些方法的对比分析得出:实际气体行为与绝热不可逆膨胀的假设得出的结果更接近真实的实验数据,而其他假设均相对保守[28,40-44]。2017 年,Hemmatian 等[45]基于该假设发现了机械能量与爆炸时刻的温度、液体填充度之间的线性关系,提出了更简捷的机械能量多项式拟合方法,避免了考虑液体的热力学性质。BLEVE 释放的机械能量除了转化为爆炸冲击波,还包括容器破裂能量、碎片变形能、碎片抛射动能、环境耗散能量等。爆炸冲击波能量所占百分比β从容器脆性断裂(很少见)的80%到韧性断裂(最常见情况) 的40%[28]。由Ew计算爆炸冲击波超压的常用方法有TNT 曲线、Sachs 曲线及Kinney &Graham经验公式。

相比于经验公式法,数值方法考虑了气体动力学过程,更接近实际。2008 年,van den Berg[46]基于液体蒸发与气液混合物膨胀速度相同的假设,通过数值计算建立了新的 BLEVE 超压和冲量曲线。2015年,Laboureur等[47]应用van den Berg的BLEVE超压和冲量曲线,建立了基于初始超压与爆炸半径的BLEVE超压计算方法
(3)凝聚相爆炸
凝聚相爆炸的物质主要是 TNT 等炸药及固体反应物。凝聚相爆炸的爆炸冲击波强度计算方法是TNT当量法,计算过程见表2。凝聚相爆炸的TNT当量法应用广泛,例如:2010年,孔德森等[48]利用TNT 当量法研究了炸药对地铁结构的破坏。2011年,范俊余等[49]采用实验与数值模拟研究了岩石乳化炸药的TNT当量系数。2015年,刘玲等[50]通过实验与TNT当量法计算了自制炸药的TNT当量。
综上可知,VCE、BLEVE、凝聚相爆炸的爆炸冲击波强度计算方法主要是在爆炸总能量及爆炸冲击波能量基础上采用 TNT 当量法或 TNO 多能法计算出爆炸冲击波强度参数。由于采用相同的方法,最终得到的不同爆炸类型的超压时程曲线特征相同。然而,张网等[26]指出:相比于凝聚相爆炸,对于小于30kPa的超压,VCE具有更长的持续时间和更大的冲量。路胜卓[51]也同样说明:与凝聚相爆炸相比,VCE 在超压相同的条件下持续时间更长,破坏效应更大。实际中由于事故场景的几何特性和爆炸总能量的不同,不同爆炸类型产生的爆炸冲击波具有不同的持续时间、峰值超压等曲线特征[6]。由于爆炸冲击波持续时间、峰值超压等特征不同,不同爆炸类型具有不同的超压、冲量。根据1.3节的超压-冲量准则,不同爆炸类型产生的结构破坏响应不同。Artero-Guerrero 等[52]的研究也指出不同的爆炸冲击波动态变化引起的结构响应不同。同 时,李波[53]、van der Voort等[54]、李丽萍等[55]的实验分别表明了 VCE、BLEVE、凝聚相爆炸的超压时程曲线可通过实验测得。因此,可开展不同爆炸类型的冲击波超压信号实验,研究不同爆炸类型的爆炸冲击波超压时程曲线特征。
1.3 爆炸冲击波的毁伤准则
爆炸冲击波的毁伤效应与爆炸冲击波超压、冲 量、各频段的能量分布、目标的自振频率有关。爆炸冲击波的一般毁伤准则分为超压准则、冲量准则、超压-冲量准则3种[56],适用范围见表5。超压准则[57]将冲击波超压作为目标伤害的唯一标准,但毁伤效应也与正相持续时间有关,时间越长则破坏越大。冲量准则认为爆炸冲击波能否对目标造成伤害完全取决于冲量,但是超压很小时正压作用时间再长也不会造成伤害[58]。超压-冲量准则综合考虑了超压和冲量,当超压和冲量同时满足临界条件时,目标才被破坏。

然而,实验表明超压和冲量越大,毁伤效应不一定越高。毁伤效应还与冲击波高低频段的能量分布、目标的自振频率有关[59-60]。2008 年,温华兵等[61-62]研究了水下爆炸压力时频分布和能量分布规律,水下爆炸压力的低频段能量接近总能量的一半,是自振频率为数十赫兹的舰船设备产生破坏的主要能源。2010年,孔霖等[63]通过实验得到了几种不同爆炸冲击波的能量谱,结果表明:能量谱在某频段的幅值越高,对自振频率在该频段的目标破坏作用越大。2015年,李丽萍等[55]提取出了同种炸药在不同爆心距、不同炸药在相同爆心距的爆炸冲击波压力信号能量频谱特性,认为同种炸药下爆炸冲击波的低频段能量大于高频段能量,毁伤范围更大,不同炸药的爆炸冲击波高、低频能量分布不同。因此,低频段能量是爆炸冲击波远距离破坏的主要原因,且与目标的固有频率有关。但相应的能量准则欠缺,可通过实验进一步开展爆炸冲击波能量谱规律研究。
2 爆炸冲击波作用下化工设备破坏失效的动力响应
2.1 化工设备的爆炸荷载加载方式
备外表面由爆炸冲击波引起的爆炸荷载导致的设备破坏失效。爆炸荷载的加载方式主要包括 3 种。①以爆炸冲击波强度参数代替设备的破坏失效。2009年,张新梅[64]将峰值超压经验公式与正反射超压公式相结合表征对设备的破坏作用。2010年,周成[65]从爆炸冲击波峰值超压、持续时间、冲量的角度研究了爆心距对设备破坏作用的影响。②将爆炸荷载作为动力加载求解设备的动力响应,如经验爆炸荷载模型或压力时程曲线等[66]。2008年,潘旭海等[67]通过数值模拟将爆炸荷载加载到圆柱形薄壁储罐,研究储罐的屈服失效过程。2011年,朱正洋[68]通过数值模拟获得了双曲线型壳体结构外表面的超压荷载,并将该荷载加载到双曲线型冷却塔,研究其动力响应。2013年,王春梅[69]将理想三角形爆炸荷载施加到有限元模型的不同单元,研究爆炸荷载下 LNG 储罐的应力与加速度响应。③利用流固耦合算法,求解爆炸荷载作用下设备的动力响应。路胜卓[51]、李波[53]运用流固耦合算法研究了浮顶罐与拱顶罐的爆炸动力响应与破坏失效机理。Zhang等[70]通过流固耦合算法模拟了爆炸荷载下球罐的动力响应。
2.2 动力响应的外界激励和变化状态
爆炸荷载作用下化工设备动力响应的主要研究方法是有限元软件。目前,关于爆炸荷载作用下的化工设备主要集中在储罐 (包括拱顶罐、浮顶罐、球罐等)、双曲线型冷却塔等壳体结构。在众多学者的研究中[57,69,71-74],爆炸荷载作用下化工设备动力响应的外界激励主要包括爆炸荷载加载位置、作用面积、作用时间等相关爆炸强度参数与储罐类型、储罐容量、储罐高径比、储罐顶盖形式、储液类型及液位高度等相关设备抗性参数,由外界激励引起的结构变化状态主要包括结构的破坏模式、爆炸荷载 (压力) 分布、应力分布、位移、加速度、应 变、结构振动加速度、能量分布等。研究主要是通过参数的时程曲线或强度分布定性分析设备破坏失效特征,但与实际事故场景相比,有待研究的外界激励还包括同时或延时的多爆炸源、爆炸源高度与距离、设备类型、连接管道、保护结构等。
关于激励条件与变化状态之间的动力响应定量研究较少。2012 年,路胜卓[51]根据质点系定量原理,建立了储罐罐壁质点沿径向运动的加速度、速度和位移与冲量之间的定量表达式,得出爆炸冲击波及罐内液体与罐壁耦合作用产生的冲量是导致罐体失稳破坏的主要原因。2015 年,Salzano 等[75]以Johnson 破坏数模型表征爆炸冲击波的破坏效应,考虑了爆炸冲击波冲量和设备材料及结构参数。表 6为2种动力响应定量模型的对比。但是已有研究涉及的外界激励较少,不能充分表征动力响应规律。而动力响应模型包括以全尺寸或对称等分尺寸几何建模为基础的空间分布参数模型及以少量节点代替响应参数详细空间分布的集中参数模型[76]。前者偏微分方程复杂,而后者主要是常微分方程,求解相对简单,路胜卓、Salzano等的模型属于后者。目前,空间分布参数模型主要以有限元软件进行建模求解。众多学者利用空间分布参数模型得出动力响应的定量关系。例如:吴家俊等[77]建立了地下密闭空间爆炸的空间分布参数模型 (即有限元模型),得出了冲击波超压与密闭空间深度之间的定量响应关系。纪冲等[78]通过圆柱壳局部冲击的空间分布参数模型 (即有限元模型),得出了圆柱壳临界破裂速度与周向撞击角的定量响应关系。同样,贾梅生等[79]运用集中参数模型定量表征了火灾环境设备热响应。因此,为了综合考虑爆炸冲击波强度参数与设备抗性参数,定量化表征强度参数与抗性参数对设备破坏失效动力响应的影响,需要通过空间分布参数模型或集中参数模型开展动力响应的定量研究。

3 爆炸冲击波作用下化工设备破坏失效概率计算方法
爆炸冲击波作用下化工设备破坏失效概率计算方法主要包括 3 种 (表 7):第 1 种是超压阈值方法,核心是静态峰值超压阈值。已有研究提出的静态峰值超压阈值并不统一,变化范围 7~70kPa[6],不确定性的原因是不同的研究考虑的设备破坏因素(容器破裂、容器位移、容器连接处位移等) 不 同。1998年,Gledhill和Lines[80]提出的常压容器与压力容器的静态峰值超压阈值分别为 7kPa 和38kPa。Khan和Abbasi[5]将70kPa作为所有设备的静态峰值超压阈值。

第2种是比例方法,核心是以静态峰值超压阈值确定最大影响距离。1991年,Bagster和Pitblado[81]提出了爆心距与爆炸冲击波最大影响距离的比例方法,该方法存在的问题是爆源附近的破坏失效概率可能小于1,与实际爆源附近的概率一定等于1不 符。2001年Cozzani等[7]提出了改进的比例方法,确定了破坏失效概率等于1的爆源范围,使其更接近实际。第3种是Probit模型方法,核心是根据设备破坏失效的严重程度定义破坏失效概率。Probit模型的数据库统计了不同设备的破坏失效严重程度及相应 的 静 态 峰 值 超 压 。1998 年 , Khan 等[5,82,85] 在Eisenberg等[86]的Probit模型基础上,以有效压力代替峰值超压,其他参数不变,但忽略了不同设备类型之间的差异性,与数据库样本的误差达 500%。研究表明不同设备类型的峰值超压破坏阈值的变化范围超过一个量级[87]。2004年,Cozzani等[7,21,88-89]定义了3种设备破坏失效的严重程度,并将设备分为常压容器、压力容器、塔设备、辅助设备4类,得到了不同设备类型的 Probit 模型,提高了 Probit 模型的准确性,与数据库样本的误差降为 55.09%。其中常压容器的Probit模型与Khan的Probit模型相近,间接说明了考虑不同设备类型的准确性。2008年,Zhang等[83]重新定义了设备破坏失效严重程度,设备类型保持不变,与数据库样本的误差降为14.1%。2013 年,Sun 等[90]将设备破坏失效严重程度作为随机参数变量,验证了Zhang 的Probit 模型的合理性和有效性。
由于设备分类不充分,Cozzani与Zhang的同一类型的设备之间存在较大(或较小)的破坏失效概率对应较小 (或较大) 的静态峰值超压等问题。2017 年,Mukhim 和 Abbasi 等[84]针对该问题,将设备进一步细分为13类,并扩展了设备破坏失效严重程度,得到的Probit模型回归系数均在0.8以上,但与数据库样本的误差有所增大,主要原因除了数据样本的差异性,还包括不同材料或尺寸的同类型设备抗冲击能力的差异性。
综上可知,3 种方法均以事故数据统计为基础,精确性依赖于数据样本的数量以及一致性,忽略了冲击波与设备之间复杂的动力响应过程。以静态峰值超压的表征方式过于简化,未充分考虑正相持续时间、冲量等其他强度参数、设备的抗性特征以及冲击波的作用过程和作用方式。根 据1.3节的爆炸冲击波的毁伤准则可知,毁伤效应不仅与超压有关,也与正相持续时间有关,时间越长则破坏越大,说明了正相持续时间、冲量等其他强度参数对动力响应过程的重要影响。不同设备具有不同的结构参数、材料参数等抗性参数,路胜卓等[51]开展了爆炸冲击波作用下不同尺寸的拱顶罐与浮顶罐缩比试验,结果得出拱顶罐之间、浮顶罐之间的动态应变、振动加速度等响应不同,表明了设备抗性参数对动力破坏响应的作用。同 时,Cozzani等[6]指出冲击波与设备之间的流固耦合作用存在着反射、绕流、流体分离等复杂现象,冲击波与设备之间的作用过程和作用方式对动力响应存在重要影响。第2节中指出,空间分布参数模型或集中参数模型可定量化表征强度参数与抗性参数对设备破坏失效动力响应的影响。因此,以空间分布参数模型或集中参数模型为基础,结合设备的破坏失效准则建立极限状态方程,通过确定随机参数分布形成相应的随机有限元法或集中参数的可靠性方法,构建基于结构可靠性的破坏失效概率计算方法,分析动力响应过程的不确定性,提高爆炸冲击波多米诺效应定量风险评的精确性。
4 爆炸冲击波作用下化工设备的易损性分析
“易损性”表达的是结构对爆炸冲击波外部破坏的抵抗能力。易损性分析的本质是基于破坏失效概率计算方法的易损性参数与概率之间的敏感性研究,易损性参数主要包括爆炸冲击波强度参数与设备抗性参数。由于现有的概率计算方法 (第3节)仅考虑了静态峰值超压与设备类型,导致分析的易损性参数较少,欠缺系统性。2004年,Cozzani等[7]在分析了爆炸冲击波作用下4种设备类型的静态峰值超压(包括由超压推导的比例距离等)的易损性曲线,结果表明:压力容器的破坏失效概率较低,相同破坏失效概率下常压容器的比例距离大于压力容器的 3 倍。2015 年,Salzano 等[75]提出的 Johnson破坏数模型综合了爆炸冲击波强度参数与设备材料参数,得出Johnson 破坏数与爆炸能量、TNT 当量之间的易损性曲线,但未考虑设备材料参数的不确定性对设备破坏失效的影响。2017 年,Mukhim等[84]建立了 13 种类型设备的静态峰值超压易损性曲线,得出压力容器 0~100% 破坏失效概率对应的静态峰值超压范围较窄,原因是压力容器抗冲击能力强,但一旦发生破坏,会迅速破裂分解。
第3节提出的基于结构可靠性的破坏失效概率计算方法,充分考虑了爆炸冲击波强度参数和设备抗性参数对破坏失效动力响应的影响。因此,根据该破坏失效概率计算方法,可进一步开展爆炸冲击波强度参数和设备抗性参数的易损性分析。
5 当前研究不足与展望
(1) 不同爆炸类型的破坏强度表征方法欠精确。采用 TNT 当量法或 TNO 多能法等相同方法导致不同爆炸类型的超压时程曲线特征相同。实际中,不同爆炸类型具有不同的升降压时间、正负相持续时间等超压时程曲线特征。各频段的能量分布也是影响爆炸冲击波毁伤的因素之一。可以通过实验进一步研究不同爆炸类型的超压时程曲线特征与能量频谱规律。
(2)缺少化工设备动力响应的定量研究。目前爆炸冲击波作用下化工设备动力响应定性研究较多,已有定量研究涉及的外界激励较少。应综合考虑爆炸冲击波强度参数与设备抗性参数,开展空间分布参数模型或集中参数模型的定量研究,表征动力响应规律。
(3)破坏失效概率计算方法过于简化。当前研究一方面以超压表征设备破坏失效的方式过于简化,另一方面基于事故数据的统计方法忽略了冲击波与设备之间复杂的动力响应过程。因此,结合动力响应集中参数模型或借鉴随机有限元法,建立基于结构可靠性的破坏失效概率计算方法是进一步的研究方向。
(4) 化工设备的易损性分析参数缺乏系统性。除了当前研究的超压、设备类型等参数,需要进一步开展爆炸冲击波强度参数、设备抗性参数的易损性研究,进而系统识别影响设备破坏失效的关键性参数,为爆炸冲击波多米诺效应防控提供参考。
在上述研究不足与展望的基础上,从爆炸冲击波强度表征、化工设备破坏失效的动力响应、破坏失效概率计算方法、易损性分析等4个方面进一步提出爆炸冲击波作用下化工设备易损性研究的流程图(图1)。
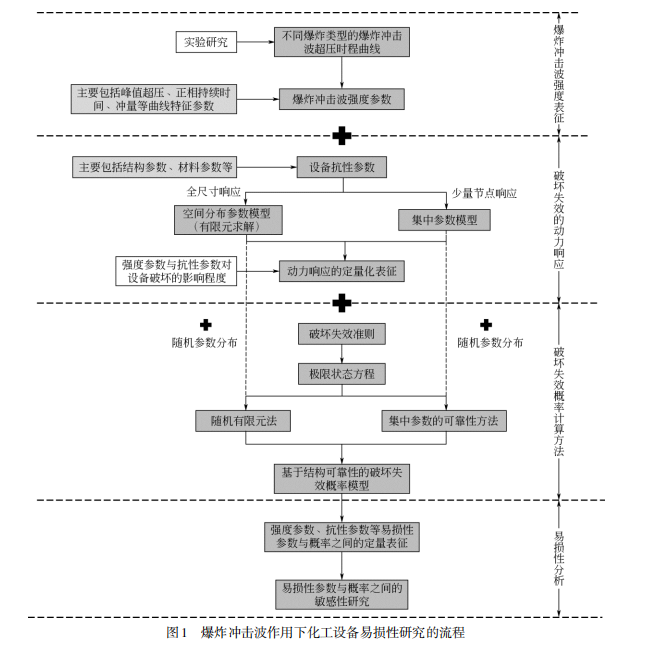
具体步骤如下:
(1)通过实验研究获取不同爆炸类型的爆炸冲击波超压时程曲线,提取出爆炸冲击波强度参数,主要包括峰值超压、正相持续时间、冲量等曲线特征参数。
(2)基于爆炸冲击波强度参数曲线与主要包括结构参数、材料参数等的设备抗性参数,采用全尺寸响应的空间分布参数模型或少量节点响应的集中参数模型,开展强度参数与抗性参数对设备破坏失效的影响程度的确定性分析,实现爆炸冲击波作用下设备动力响应的定量化表征。
(3)基于结构可靠性理论,在定量化的动力响应模型基础上结合设备的破坏失效准则,建立相应的极限状态方程,通过确定随机参数分布,形成随机有限元法(对应空间分布参数模型)或集中参数的可靠性方法 (对应集中参数模型),最终构建破坏失效概率模型。
(4)通过概率模型确定强度参数、抗性参数等易损性参数与概率之间的定量表征关系,进而开展易损性参数的敏感性研究。综上可知,爆炸冲击波作用下化工设备易损性研究的核心是设备破坏失效概率计算方法,该方法表征设备动力响应的程度决定了概率计算的精确性及易损性分析的系统性。而通过集中参数的可靠性方法或随机有限元法能够充分揭示动力响应规律并表征概率。因此,集中参数的可靠性方法与随机有限元法是提高易损性研究可靠性与精确性的关键性研究方向,进而为爆炸冲击波多米诺效应定量风险评估提供更精确的结果,为爆炸冲击波多米诺效应防控提供更全面的参考措施。
6 结语
本文从爆炸冲击波强度表征、化工设备破坏失效的动力响应、破坏失效概率计算方法、易损性分析4个方面对国内外研究现状进行分类、评述。指出了不同爆炸类型的破坏强度表征方法欠精确、缺少化工设备动力响应的定量研究、破坏失效概率计算方法过于简化、化工设备的易损性分析参数缺乏系统性等当前研究存在的不足。并提出了不同爆炸类型的超压时程曲线特征与能量频谱规律研究、空间分布参数模型或集中参数模型的定量研究、基于结构可靠性的破坏失效概率计算方法、爆炸冲击波强度参数与设备抗性参数的易损性分析等进一步研究的展望。在不足与展望基础上系统性建立了爆炸冲击波作用下化工设备易损性研究的流程图。最终指出集中参数的可靠性方法与随机有限元法是提高设备易损性研究可靠性与精确性的关键性研究方向,以期更精确地评估爆炸冲击波多米诺效应定量风险并提出更全面的防控措施。
参考文献
[1] Center for Chemical Process Safety(CCPS). Guidelines for chemicalprocess quantitative risk analysis[M]. 2nd ed. New York: AmericanInstitute of Chemical Engineers, 2000.
[2] 贾梅生, 陈国华, 胡昆. 化工园区多米诺事故风险评价与防控技术综述[J]. 化工进展, 2017, 36(4): 1534-1543.JIA Meisheng, CHEN Guohua,HU Kun. Review of risk assessmentand pro-control of Domino effect in Chemical Industry Park[J].Chemical Industry and Engineering Progress, 2017, 36(4): 1534-1543.
[3] DELVOSALLE C. Domino effects phenomena: definition, overview andclassification[C]// European Seminar on Domino Effects, Brussels,1996: 5-15.
[4] MHIDAS. Major Hazard incident data service [DB]. AES Health andSafety Executive, UK, 2001.
[5] KHAN F I, ABBASI S A. Models for domino effect analysis inchemical process industries[J]. Process Safety Progress, 1998, 17(2):107-123.
[6] COZZANI V, GUBINELLI G, SALZANO E. Escalation thresholds inthe assessment of Domino accidental events[J]. Journal of HazardousMaterials, 2006, 129(1/2/3): 1-21.
[7] COZZANI V, SALZANO E. The quantitative assessment of Dominoeffects caused by overpressure: Part I. Probit models[J]. Journal ofHazardous Materials. 2004, 107(3): 67-80.
[8] STAWCZYK J. Experimental evaluation of LPG tank explosion hazards[J]. Journal of Hazardous Materials, 2003, 96(2): 189-200.
[9] JIANG J C, LIU Z G, KIM A K. Comparison of blast prediction modelsfor vapor cloud explosion[C]// The Combustion Institute / CanadaSection, 2001 Spring Technical Meeting, 2001.
[10] BAKER Q A, BAKER W E. Pros and cons of TNT equivalence forindustrial explosion accidents[C]// Proceedings of the InternationalConference and Workshop on Modeling and Mitigating theConsequences of Accidental Releases of Hazardous Materials, 1991.
[11] VAN DEN BERG A C. The multi-energy method: a framework forvapour cloud explosion blast prediction[J]. Journal of HazardousMaterials, 1985, 12(1): 1-10.
[12] STREHLOW R A, LUCKRITZ R T, ADAMCZYK A A, et al. The blastwave generated by spherical flames[J]. Combustion & Flame, 1979, 35(79): 297-310.
[13] 沙金成. 立式固定拱顶储罐爆炸压力下的结构应力分析[D]. 大庆:东北石油大学, 2014.SHA Jincheng. Structural stress analysis of vertical fixed-roof storagetanks under explosion pressure [D]. Daqing: Northeast PetroleumUniversity, 2014.
[14] 严景艺, 张礼敬, 陶刚. 瓶装液化气钢瓶泄漏事故[J]. 安全, 2016, 37(8): 42-44.YAN Jingyi, ZHANG Lijing, TAO Gang. Bottle liquefied gas cylinderleakage accident[J]. Safety, 2016, 37(8): 42-44.
[15] 管义锋, 史腾飞, 朱培培, 等. LNG双燃料船舶加注过程气罐泄漏爆炸后果分析[J]. 船舶工程, 2016(1): 31-34.GUAN Yifeng, SHI Tengfei, ZHU Peipei, et al. Analysis on explosionconsequence due to gas tank leakage in fuel filling process for LNGdouble-fuelled ship[J]. Ship Engineering, 2016(1): 31-34.
[16] 丁宇奇, 戴希明, 刘巨保, 等. 基于TNT当量法的储罐内爆压力简化计算与应力分析[J]. 数学的实践与认识, 2017, 47(8): 116-126.DING Yuqi, DAI Ximing, LIU Jubao, et al. Simplified calculation oftank explosion pressure based on TNT method and stress analysis[J].Mathematics in Practice and Theory, 2017, 47(8): 116-126.
[17] VAN DEN BOSCH C J H, WEJERINGS R A P M. Methods for thecalculation of physical effects-due to the releases of hazardous material(liquid and gases)—‘Yellow Book’[M]. 3rd ed. The Hague: AdvisoryCouncil on Dangerous Substances, 2005.
[18] MERCX W P M, VAN DEN BERG A C, HAYHURST C J, et al.Developments in vapour cloud explosion blast modeling[J]. Journal ofHazardous Materials, 2000, 71(1): 301-319.
[19] MAREMONTI M, RUSSO G, SALZANO E, et al. Post-accidentanalysis of vapour cloud explosions in fuel storage areas[J]. ProcessSafety & Environmental Protection, 1999, 77(6): 360-365.
[20] LOBATO J, CAÑIZARES P, RODRIGO M A, et al. A comparison ofhydrogen cloud explosion models and the study of the vulnerability ofthe damage caused by an explosion of H2[J]. International Journal ofHydrogen Energy, 2006, 31(12): 1780-1790.
[21] SALZANO E, COZZANI V. The analysis of domino accidents triggeredby vapor cloud explosions[J]. Reliability Engineering & System Safety,2005, 90(2): 271-284.
[22] ALONSO F D, FERRADÁS E G, PÉREZ J F S, et al. Characteristicoverpressure-impulse-distance curves for vapour cloud explosionsusing the TNO multi-energy model[J]. Journal of Hazardous Materials,2006, 137(2): 734-741.
[23] ALONSO F D, FERRADÁS E G, DE JESÚS JIMÉNEZ SÁNCHEZA T,et al. Consequence analysis to determine the damage to humans fromvapour cloud explosions using characteristic curves[J]. Journal ofHazardous Materials, 2008, 150(1): 146-152.
[24] ALONSO F D, FERRADÁS E G, PÉREZ J F S, et al. Consequenceanalysis to determine damage to buildings from vapour cloudexplosions using characteristic curves[J]. Journal of HazardousMaterials, 2008, 159(2): 264-270.
[25] TANG M J, BAKER Q A. A new set of blast curves from vapor cloudexplosion[J]. Process Safety Progress, 1999, 18(4): 235-240.
[26] 张网, 吕东, 王婕. 蒸气云爆炸后果预测模型的比较研究[J]. 工业安全与环保, 2010, 36(4): 48-49.ZHANG Wang, LÜ Dong, WANG Jie. Comparison of vapor cloudexplosion consequences prediction models[J]. Industrial Safety andEnvironmental Protection, 2010, 36(4): 48-49.
[27] SARI A. Comparison of TNO multienergy and Baker-Strehlow-Tangmodels[J]. Process Safety Progress, 2015, 30(1): 23-26.
[28] HEMMATIAN B, PLANAS E, CASAL J. Comparative analysis ofBLEVE mechanical energy and overpressure modelling[J]. ProcessSafety & Environmental Protection, 2017, 106: 138-149.
[29] BRODE H L. Blast wave from a spherical charge[J]. The Physics ofFluids, 1959, 2(2): 217-229.
[30] PRUGH R W. Quantitative evaluation of BLEVE hazards[J]. Journal ofFire Protection Engineering, 1991, 3(1): 9-24.
[31] CROWL D A. Using thermodynamic availability to determine theenergy of explosion[J]. Process Safety Progress, 1991, 10(3): 136-142.
[32] CROWL D A. Using thermodynamic availability to determine theenergy of explosion for compressed gases[J]. Process Safety Progress,1992, 11(2): 47-49.
[33] SMITH J M. VAN NESS H C, ABBOTT M M. Introduction to chemicalengineering thermodynamics[M]. 8th ed. New York: McGraw-HillHiger Education, 2017.
[34] PLANAS-CUCHI E, SALLA J M, CASAL J. Calculating overpressurefrom BLEVE explosions[J]. Journal of Loss Prevention in the ProcessIndustries, 2004, 17(6): 431-436.
[35] CASAL J, SALLA J M. Using liquid superheating energy for a quickestimation of overpressure in BLEVEs and similar explosions[J].Journal of Hazardous Materials, 2006, 137(3): 1321-1327.
[36] ROBERTS M W. Analysis of boiling liquid expanding vapor explosion(BLEVE) events at DOE sites[C]// Proceedings SA-2000 SafetyAnalysis Working Group Workshop 2000. Los Alamos. Los AlamosNational Laboratory, 2000.
[37] Center for Chemical Process Safety (CCPS). Guidelines for vapor cloudexplosion, pressure vessel burst, BLEVE, and flash fire hazards[M].2nd ed. New York: Wiley Subscription Services, Inc., 2010.
[38] GENOVA B, SILVESTRINI M, LEON TRUJILLO F J. Evaluation ofthe blast-wave overpressure and fragments initial velocity for aBLEVE event via empirical correlations derived by a simplified modelof released energy[J]. Journal of Loss Prevention in the ProcessIndustries, 2008, 21(1): 110-117.
[39] BIRK A M, DAVISON C, CUNNINGHAM M. Blast overpressures frommedium scale BLEVE tests[J]. Journal of Loss Prevention in theProcess Industries, 2007, 20(3): 194-206.
[40] ABBASI T, ABBASI S A. The boiling liquid expanding vapourexplosion (BLEVE): mechanism, consequence assessment, management[J]. Journal of Hazardous Materials, 2007, 141(3): 489-519.
[41] BUBBICO R, MARCHINI M. Assessment of an explosive LPG releaseaccident: a case study[J]. Journal of Hazardous Materials, 2008, 155(3): 558-565.
[42] CROWL D A. Understanding explosions[M]. New York: AmericanInstitute of Chemical Engineers(AIChE), 2010.
[43] OGLE R A, RAMIREZ J C, SMYTH S A. Calculating the explosionenergy of a boiling liquid expanding vapor explosion using exergyanalysis[J]. Process Safety Progress, 2012, 31(1): 51-54.
[44] LABOUREUR D, HEYMES F, LAPEBIE E, et al. BLEVEoverpressure: multiscale comparison of blast wave modeling[J]. ProcessSafety Progress, 2014, 33(3): 274-284.
[45] HEMMATIAN B, CASAL J, PLANAS E. A new procedure to estimateBLEVE overpressure[J]. Process Safety & Environmental Protection,2017, 111: 320-325.
[46] VAN DEN BERG A C. Blast charts for explosive evaporation ofsuperheated liquids[J]. Process Safety Progress, 2008, 27(3): 219-224.
[47] LABOUREUR D, BIRK A M, BUCHLIN J M, et al. A closer look atBLEVE overpressure[J]. Process Safety & Environmental Protection,2015, 95: 159-171.
[48] 孔德森, 张伟伟, 孟庆辉, 等. TNT当量法估算地铁恐怖爆炸中的炸药当量[J]. 地下空间与工程学报, 2010, 6(1): 197-200.KONG Desen, ZHANG Weiwei, MENG Qinghui, et al. Estimation andevaluation of terror explosion equivalent in underground by TNTequivalent[J]. Chinese Journal of Underground Space and Engineering,2010, 6(1): 197-200.
[49] 范俊余, 方秦, 张亚栋,等. 岩石乳化炸药TNT当量系数的试验研究[J]. 兵工学报, 2011, 32(10): 1243-1249.FAN Junyu, FANG Qin, ZHANG Yadong, et al. Experimental study onTNT equivalent coefficient of rock emulsion explosives[J]. ActaArmamentarii, 2011, 32(10): 1243-1249.
[50] 刘玲, 袁俊明, 刘玉存,等. 自制炸药的冲击波超压测试及TNT当量估算[J]. 火炸药学报, 2015, 38(2): 50-53.LIU Ling, YUAN Junming, LIU Yucun, et al. Measurement of shockwave overpressure and TNT equivalent of homemade explosives[J].Chinese Journal of Explosives & Propellants, 2015, 38(2): 50-53.
[51] 路胜卓. 可燃气体爆炸作用下大型钢制储油罐破坏机理研究[D].哈尔滨:哈尔滨工业大学, 2012.LU Shengzhuo. Research on failure mechanism of large-scale steel oilstorage tanks under combustible gas blast [D]. Harbin: Harbin Instituteof Technology, 2012.
[52] ARTERO-GUERRERO J, PERNAS-SÁNCHEZ J, TEIXEIRA-DIASF. Blast wave dynamics: the influence of the shape of the explosive[J].Journal of Hazardous Materials, 2017, 331: 189-199.
53] 李波. 爆炸荷载作用下大型立式圆柱形储油罐动力响应分析[D].哈尔滨:哈尔滨工业大学, 2011.LI Bo. Analysis of dynamic response of large-scale liquid-storagevertical cylindrical tank under blast loads [D]. Harbin: Harbin Instituteof Technology, 2011.
[54] VAN DER VOORT M M, VAN DEN BERG A C, ROEKAERTS D J EM, et al. Blast from explosive evaporation of carbon dioxide:experiment, modeling and physics[J]. Shock Waves, 2012, 22(2):129-140.
55] 李丽萍, 孔德仁, 苏建军, 等. 基于能量谱的爆炸冲击波毁伤特性研究[J]. 振动与冲击, 2015, 34(21): 71-75.LI Liping, KONG Deren, SU Jianjun, et al. Damage effects analysis forexplosion shock wave based on energy spectrum[J]. Journal ofVibration and Shock, 2015, 34(21): 71-75.
[56] 张守中. 爆炸与冲击动力学[M]. 北京: 兵器工业出版社, 1993.ZHANG Shouzhong. Explosion and shock dynamics [M]. Beijing: ThePublishing House of Ordnance Industry, 1993.
[57] 李秋媛. 化工设备区爆炸冲击波传递影响研究[D]. 哈尔滨:哈尔滨理工大学, 2014.LI Qiuyuan. Research on propagation rules of blast shock wave inchemical plant area [D]. Harbin: Harbin Institute of Technology, 2014.
[58] 吴宗之, 高进东, 魏利军, 等. 危险评价方法及其应用[M]. 北京: 冶金工业出版社, 2001.WU Zongzhi, GAO Jindong, WEI Lijun, et al. Risk assessmentmethods and applications [M]. Beijing: Metallurgical Industry Press,2001.
[59] JEREMIĆ R, BAJIĆ Z. An approach to determining the TNTequivalent of high explosives[J]. Scientific Technical Review, 2006, lvi(1): 58-62.
[60] 曹凤霞. 爆炸综合毁伤效应研究[D]. 南京:南京理工大学, 2008.CAO Fengxia. Study on multi-damage effect of explosion [D]. Nanjing:Nanjing University of Science & Technology, 2008.
[61] 温华兵, 尹群, 张健. 水下爆炸压力时频分布的小波包分析[J]. 江苏科技大学学报(自然科学版), 2008, 22(5): 48-52.WEN Huabing, YIN Qun, ZHANG Jian. Analysis of time-frequencydistribution of underwater explosion pressure through wavelet packettransform[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2008, 22(5): 48-52.
[62] 温华兵, 张健, 尹群, 等. 水下爆炸船舱冲击响应时频特征的小波包分析[J]. 工程力学, 2008, 25(6): 199-203.WEN Huabing, ZHANG Jian, YIN Qun, et al. Wavelet packet analysisof time-frequency characteristic of cabin shock response due tounderwater explosion[J]. Engineering Mechanics, 2008, 25(6):199-203.
[63] 孔霖, 苏健军, 李芝绒, 等. 几种不同爆炸冲击波作用的能量谱分析[J]. 火炸药学报, 2010, 33(6): 76-79.KONG Lin, SU Jianjun, LI Zhirong, et al. Energy spectrum analysis ofseveral kinds of explosive blast[J]. Chinese Journal of Explosives &Propellants, 2010, 33(6): 76-79.
[64] 张新梅. 化工园区事故多米诺效应风险仿真原理及应用研究[D].广州: 华南理工大学, 2009.ZHANG Xinmei. Study on simulation principle of accident risk causedby Domino effect and its application in chemical industrial parks [D].Guangzhou: South China University of Technology, 2009.
[65] 周成. 化工园区事故多米诺效应下LPG 储罐动力学特性研究[D].广州: 华南理工大学, 2010.ZHOU Cheng. The research of dynamic characteristics on LPG storagetank of Domino effect in chemical industry park [D]. Guangzhou: SouthChina University of Technology, 2010.
[66] 李天华. 爆炸荷载下钢筋混凝土板的动态响应及损伤评估[D]. 西 安: 长安大学, 2012.LI Tianhua. Dynamic response and damage assessment of reinforcedconcrete slabs subjected to blast loading [D]. Xi’an: Chang’anUniversity, 2012.
[67] 潘旭海, 徐进, 蒋军成. 圆柱形薄壁储罐对爆炸冲击波动力学响应的模拟分析[J]. 化工学报, 2008, 59(3): 796-801.PAN Xuhai, XU Jin, JIANG Juncheng. Simulation analysis of dynamicresponse of thin-wall cylindrical tank to shock wave[J]. Journal ofChemical Industry and Engineering (China), 2008, 59(3): 796-801.
[68] 朱正洋 . 爆炸荷载作用下大型双曲线型壳体结构动力响应分析[D]. 西安:西安建筑科技大学, 2011.ZHU Zhengyang. Dynamic response of large scaled hyperbolic shellstructures under blast loading [D]. Xi’an: Xi’an University ofArchitecture and Technology, 2011.
[69] 王春梅. LNG储罐在爆炸冲击荷载作用下的动力响应及可靠性分析[D]. 天津:天津大学, 2013.WANG Chunmei. Reliability analysis and dynamic response of LNGstorage tank under explosive impact load [D]. Tianjin: TianjinUniversity, 2013.
[70] ZHANG B Y, LI H H, WANG W. Numerical study of dynamicresponse and failure analysis of spherical storage tanks under externalblast loading[J]. Journal of Loss Prevention in the Process Industries,2015, 34: 209-217.
[71] 于志华. 爆炸冲击作用下球型储液罐动力响应分析[D]. 哈尔滨:哈尔滨工业大学, 2011.YU Zhihua. Analysis of dynamic response of spherical liquid-storagetank under blast loading [D]. Harbin: Harbin Institute of Technology,2011.
[72] 胡可. 钢储罐结构爆炸冲击荷载与动力响应的数值模拟研究[D].杭州:浙江大学, 2016.HU Ke. Numerical simulation of explosion loading and dynamicresponse of steel tanks[D]. Hangzhou: Zhejiang University, 2016.
[73] 朱东. 大型钢储罐在撞击和爆炸荷载作用下的动力响应分析[D].杭州:浙江大学, 2016.ZHU Dong. The analysis of dynamic response of large steel tank underimpact and explosion load [D]. Hangzhou: Zhejiang University, 2016.
[74] 路胜卓, 王伟, 陈卫东. 浮顶式储油罐的爆炸冲击失效[J]. 爆炸与冲击, 2015, 35(5): 696-702.LU Shengzhuo, WANG Wei, CHEN Weidong. Failure characteristicsof floating-roof oil storage tanks subjected to blast impact[J].Explosion and Shock Waves, 2015, 35(5): 696-702.
[75] SALZANO E, BASCO A. Simplified model for the evaluation of theeffects of explosions on industrial target[J]. Journal of Loss Preventionin the Process Industries, 2015, 37(81): 119-123.
[76] 贾梅生. 过程设备火灾易损性理论与多米诺效应防控[D]. 广州: 华南理工大学, 2017.JIA Meisheng. Vulnerability theory for process equipment exposed tofire and pre-control of Domino effects [D]. Guangzhou: South ChinaUniversity of Technology, 2017.
[77] 陈国华, 吴家俊. 地下密闭空间燃气爆炸冲击波传播规律[J]. 天然气工业, 2017, 37(2): 120-125.CHEN Guohua, WU Jiajun. Propagation laws of gas explosion shockwaves in underground confined space[J]. Natural Gas Industry, 2017,37(2): 120-125.
[78] 纪冲, 龙源, 方向, 等. 钢质圆柱壳在侧向局部冲击荷载下的变形及失效破坏[J]. 振动与冲击, 2013, 32(15): 121-125.JI Chong, LONG Yuan, FANG Xiang, et al. Dynamic response andperforation failure of cylindrical shell subjected to lateral localimpulsive loading[J]. Journal of Vibration and Shock, 2013, 32(15):121-125.
[79] 贾梅生, 陈国华. 火灾环境液化石油气卧罐稳定性与静态可靠性分析[J]. 化工进展, 2017, 36(7): 2353-2359.JIA Meisheng, CHEN Guohua. Stability and static reliability ofhorizontal LPG tank exposed to fire[J]. Chemical Industry andEngineering Progress, 2017, 36(7): 2353-2359.
[80] GLEDHILL J, LINES I. Development of methods to assess thesignificance of domino effects from major hazard sites: contractresearch report 183 / 1998[R]. Norwich: Health and Safety Executive(HSE), 1998.
[81] BAGSTER D, PITBLADO R. Estimation of Domino incidentfrequencies – an approach[J]. Process Safety and EnvironmentProtection, 1991, 69(4): 195-199.
[82] KHAN F I, ABBASI S A. Studies on the probabilities and likelyimpacts of chains of accident (Domino effect) in a fertilizer industry[J].Process Safety Progress, 2000, 19(19): 40-56.
[83] ZHANG M G, JIANG J C. An improved Probit method for assessmentof Domino effect to chemical process equipment caused byoverpressure[J]. Journal of Hazardous Materials, 2008, 158(2):280-286.
[84] MUKHIM E D, ABBASI T, TAUSEEF S M, et al. Domino effect inchemical process industries triggered by overpressure – formulation ofequipment-specific Probits[J]. Process Safety & EnvironmentalProtection, 2017, 106: 263-273.
[85] KHAN F I, ABBASI S A. An assessment of the likelihood ofoccurrence, and the damage potential of Domino effect (chain ofaccidents) in a typical cluster of industries[J]. Journal of LossPrevention in the Process Industries, 2001, 14(4): 283-306.
[86] EISENBERG N A, LYNCH C J, BREEDING R J. Vulnerability model.A simulation system for assessing damage resulting from marine spills:report CG-D-136-75[R]. Spring Field: National TechnicalInformation Service, 1975.
[87] COZZANI V, SALZANO E. Threshold values for Domino effectscaused by blast wave interaction with process equipment[J]. Journal ofLoss Prevention in the Process Industries[J]. 2004, 17(6): 437-447.
[88] COZZANI V, SALZANO E. The quantitative assessment of Dominoeffect caused by overpressure: Part Ⅱ . Case studies[J]. Journal ofHazardous Materials, 2004, 107(3): 81-94.
[89] SALZANO E, COZZANI V. A fuzzy set analysis to estimate lossintensity following blast wave interaction with process equipment[J].Journal of Loss Prevention in the Process Industries, 2006, 19(4):343-352.
[90] SUN D L, HUANG G T, JIANG J C, et al. Study on the rationality andvalidity of Probit models of Domino effect to chemical processequipment caused by overpressure[J]. Journal of Physics ConferenceSeries, 2013, 423(1): 1-9.



